Решебник по геометрии 8 класс Атанасян ФГОС Задание 106

 

\[\boxed{\mathbf{106.ОК\ ГДЗ - домашка\ на}\ 5}\]

\[Рисунок\ по\ условию\ \mathbf{задачи:}\]

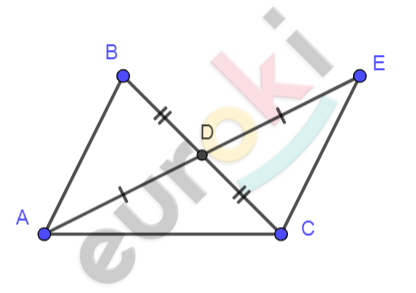
\[\mathbf{Дано:}\]

\[\mathrm{\Delta}ABC;\]

\[AD = DE;\]

\[AD - медиана;\]

\[\angle ACD = 56{^\circ};\]

\[\angle ABD = 40{^\circ}.\]

\[\mathbf{а)\ Доказать:}\]

\[\mathrm{\Delta}ABD = \mathrm{\Delta}ECD.\]

\[\mathbf{б)\ Найти:}\]

\[\angle ACE - ?\]

\[\mathbf{Решение.}\]

\[\textbf{а)}\ \mathrm{\Delta}ABD = \mathrm{\Delta}ECD - по\ двум\ \]

\[сторонам\ и\ углу\ между\ ними:\]

\[\angle BDA =\]

\[= \angle EDC\ (как\ вертикальные);\]

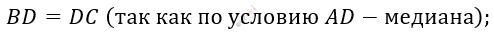
\[AD = DE\ (по\ условию).\]

\[Что\ и\ требовалось\ доказать.\]

\[\textbf{б)}\ Так\ как\ треугольники\ \]

\[равны,\ то\ и\ равные\ элементы\ \]

\[в\ них\ равны:\]

\[\angle ABD = \angle DCE = 40{^\circ}.\]

\[\angle ACE = \angle ACD + \angle DCE =\]

\[= 56{^\circ} + 40{^\circ} = 96{^\circ}.\]

\[Ответ:\angle ACE = 96{^\circ}.\]

\[\boxed{\mathbf{106.}\mathbf{еуроки - ответы\ на\ пятёрку}}\]

\[\mathbf{Рисунок\ по\ условию\ задачи:}\]