Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 9 класс Атанасян ФГОС Задание 265
Задание 265
\[\boxed{\mathbf{265.ОК\ ГДЗ - домашка\ на}\ 5}\]
\[Рисунок\ по\ условию\ задачи:\]
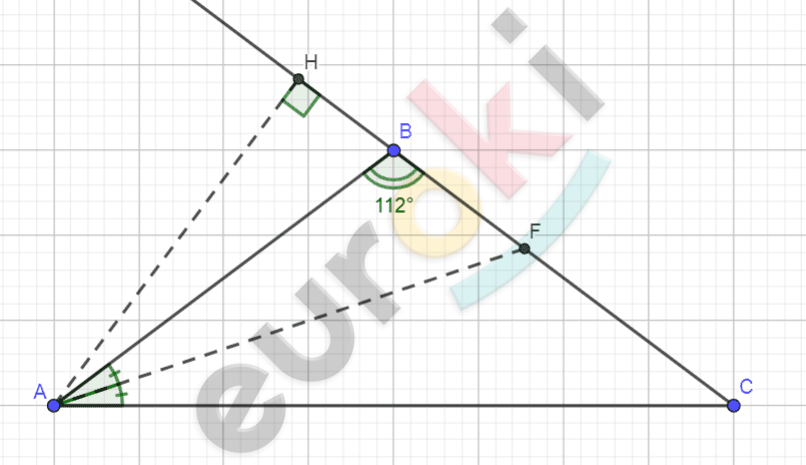
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - равнобедренный;\]
\[AB = BC;\]
\[\angle B = 112{^\circ};\]
\[AH\bot BC;\]
\[AF - биссектриса\ \angle\text{A.}\]
\[\mathbf{Найти:}\]
\[\angle HAF - ?\]
\[\angle HFA - ?\]
\[\mathbf{Решение.}\]
\[1)\ \mathrm{\Delta}ABC - равнобедренный:\]
\[\angle A = \angle C\ (по\ свойству).\]
\[2)\ \angle A = \angle C = \frac{180{^\circ} - 112{^\circ}}{2} =\]
\[= \frac{68{^\circ}}{2} = 34{^\circ}.\]
\[3)\ Так\ как\ AF - биссектриса\ \]
\[\angle A:\]
\[\angle BAF = \angle FAC = \frac{34{^\circ}}{2} = 17{^\circ}.\]
\[4)\ По\ теореме\ о\ свойстве\ углов\ \]
\[в\ треугольнике:\]
\[\angle HFA = 180{^\circ} - (112{^\circ} + 17{^\circ}) =\]
\[= 51{^\circ}.\]
\[5)\ По\ свойству\ прямоугольного\ \]
\[треугольника:\]
\[\angle HAF = 90{^\circ} - 51{^\circ} = 39{^\circ}.\]
\[\mathbf{Ответ:\ }\angle HAF = 39{^\circ};\ \]
\[\angle HFA = 51{^\circ}.\]
\[\boxed{\mathbf{265.еуроки - ответы\ на\ пятёрку}}\]
\[Рисунок\ по\ условию\mathbf{\ задачи:}\]
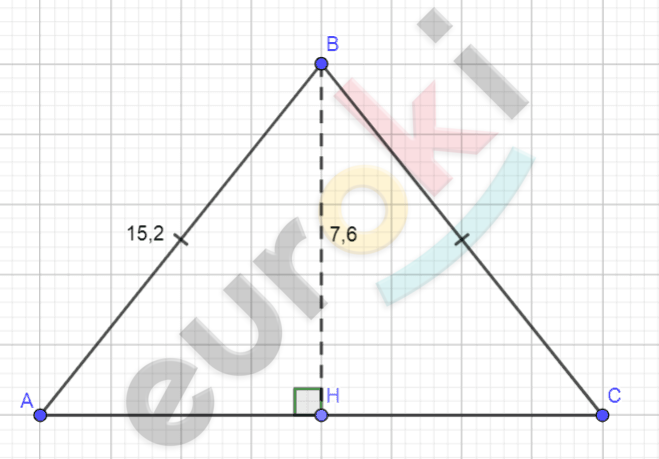
\[\mathbf{Дано:}\]
\[\mathrm{\Delta}ABC - равнобедренный;\]
\[AB = BC;\]
\[BH\bot AC;\]
\[BH = 7,6\ см;\]
\[AB = 15,2\ см.\]
\[\mathbf{Найти:}\]
\[\angle A - ?;\ \angle B - ?;\ \ \angle C - ?\]
\[\mathbf{Решение.}\]
\[1)\ BH = \frac{\text{AB}}{2} \Longrightarrow 7,6 = \frac{15,2}{2}.\]
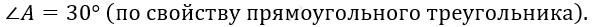
\[2)\ \mathrm{\Delta}ABC - равнобедренный:\]
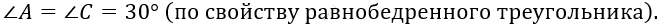
\[3)\ \angle B = 180{^\circ} - (30{^\circ} + 30{^\circ}) =\]
\[= 180{^\circ} - 60{^\circ} = 120{^\circ}.\]
\[Ответ:\ \angle A = \angle C = 30{^\circ};\ \]
\[\angle B = 120{^\circ}.\]
