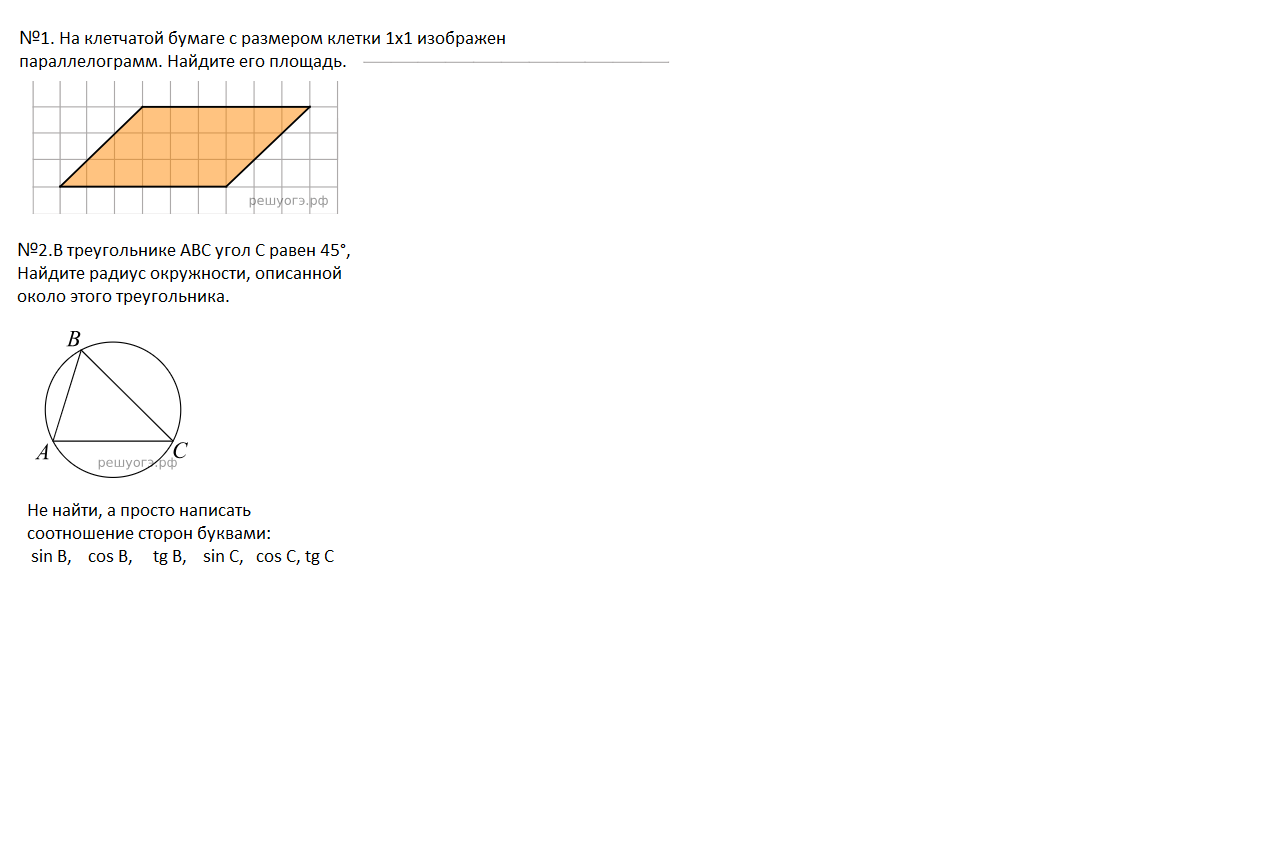
№2. В треугольнике ABC угол C равен 45°, Найдите радиус окружности, описанной около этого треугольника.

В условии задачи не хватает данных, чтобы найти точное значение радиуса окружности, описанной около треугольника ABC. Для нахождения радиуса описанной окружности нам нужно знать либо длины всех сторон треугольника, либо длину одной из сторон и противолежащий ей угол. Без этих данных, мы можем только написать общее соотношение с использованием теоремы синусов. Теорема синусов гласит, что отношение длины стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности (или удвоенному радиусу). То есть $$\frac{AB}{\sin(C)} = \frac{BC}{\sin(A)} = \frac{AC}{\sin(B)} = 2R$$, где R - радиус описанной окружности. Так как нам дан угол C, то можно записать: $$2R = \frac{AB}{\sin(45^\circ)}$$. Поскольку $$\sin(45^\circ) = \frac{\sqrt{2}}{2}$$, то $$2R = \frac{AB}{\frac{\sqrt{2}}{2}} = \frac{2AB}{\sqrt{2}} = AB\sqrt{2}$$. Отсюда радиус описанной окружности равен $$R = \frac{AB\sqrt{2}}{2}$$. Для нахождения числового значения нам нужна длинна стороны AB. Без неё мы можем только выразить радиус описанной окружности, но не можем найти его конкретное значение.