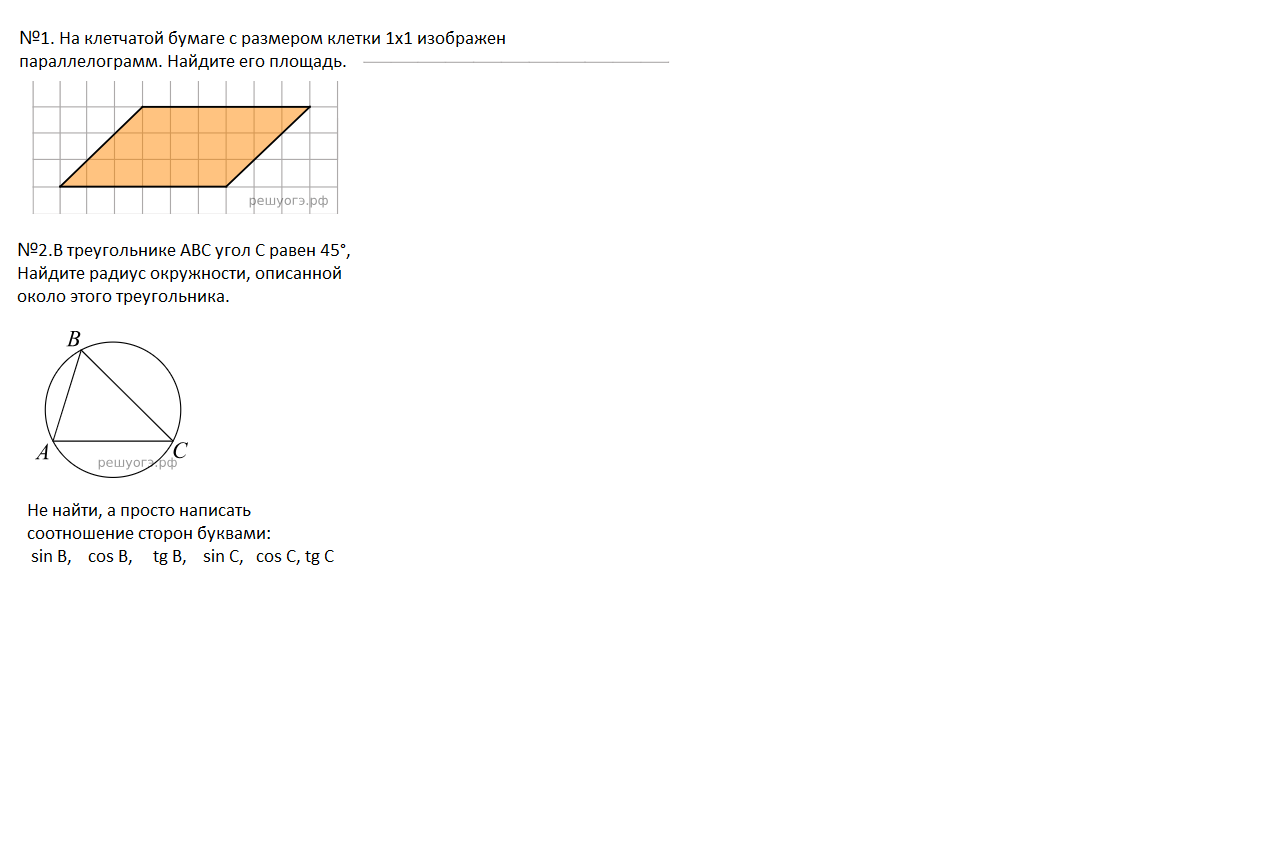
Вопрос:
Не найти, а просто написать соотношение сторон буквами: sin B, cos B, tg B, sin C, cos C, tg C
Ответ:
Здесь нужно выразить тригонометрические функции углов B и C через стороны треугольника ABC. В общем случае:
- \(\sin(B) = \frac{\text{противолежащий катет}}{\text{гипотенуза}} = \frac{AC}{AB}\)
- \(\cos(B) = \frac{\text{прилежащий катет}}{\text{гипотенуза}} = \frac{BC}{AB}\)
- \(\tan(B) = \frac{\text{противолежащий катет}}{\text{прилежащий катет}} = \frac{AC}{BC}\)
- \(\sin(C) = \frac{\text{противолежащий катет}}{\text{гипотенуза}} = \frac{AB}{BC}\)
- \(\cos(C) = \frac{\text{прилежащий катет}}{\text{гипотенуза}} = \frac{AC}{BC}\)
- \(\tan(C) = \frac{\text{противолежащий катет}}{\text{прилежащий катет}} = \frac{AB}{AC}\)
Внимание, данные определения работают для прямоугольных треугольников. В нашем случае треугольник ABC не указан, как прямоугольный, поэтому данные выражения в таком виде будут неправильными.
В общем случае, если рассматривать треугольник, не как прямоугольный, то тригонометрические выражения будут следующими:
$$\sin(B) = \frac{AC}{2R}$$,
$$\cos(B) = \frac{a^2+c^2-b^2}{2ac}$$,
$$\tan(B) = \frac{\sin(B)}{\cos(B)}$$,
$$\sin(C) = \frac{AB}{2R}$$,
$$\cos(C) = \frac{a^2+b^2-c^2}{2ab}$$,
$$\tan(C) = \frac{\sin(C)}{\cos(C)}$$
где a, b, c - соответсвенно стороны BC, AC и AB, R - радиус описанной окружности.