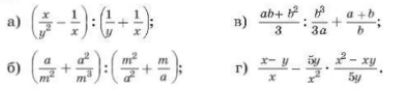
Вопрос:
б) (\frac{a}{m^{2}}+\frac{a^{2}}{m^{3}}):(\frac{m^{2}}{a^{2}}+\frac{m}{a});
Ответ:
б) Упростим выражение: $$(\frac{a}{m^{2}}+\frac{a^{2}}{m^{3}}):(\frac{m^{2}}{a^{2}}+\frac{m}{a})$$
Приведем к общему знаменателю в первой скобке:$$\frac{a}{m^{2}}+\frac{a^{2}}{m^{3}} = \frac{a \cdot m + a^{2}}{m^{3}} = \frac{a(m+a)}{m^{3}}$$
Приведем к общему знаменателю во второй скобке:$$\frac{m^{2}}{a^{2}}+\frac{m}{a} = \frac{m^{2} + m \cdot a}{a^{2}} = \frac{m(m+a)}{a^{2}}$$
Выполним деление дробей:$$\frac{a(m+a)}{m^{3}}: \frac{m(m+a)}{a^{2}} = \frac{a(m+a)}{m^{3}} \cdot \frac{a^{2}}{m(m+a)} = \frac{a(m+a) \cdot a^{2}}{m^{3} \cdot m(m+a)}$$
Сократим дроби:$$\frac{a(m+a) \cdot a^{2}}{m^{3} \cdot m(m+a)} = \frac{a^{3}}{m^{4}}$$
Ответ: $$\frac{a^{3}}{m^{4}}$$