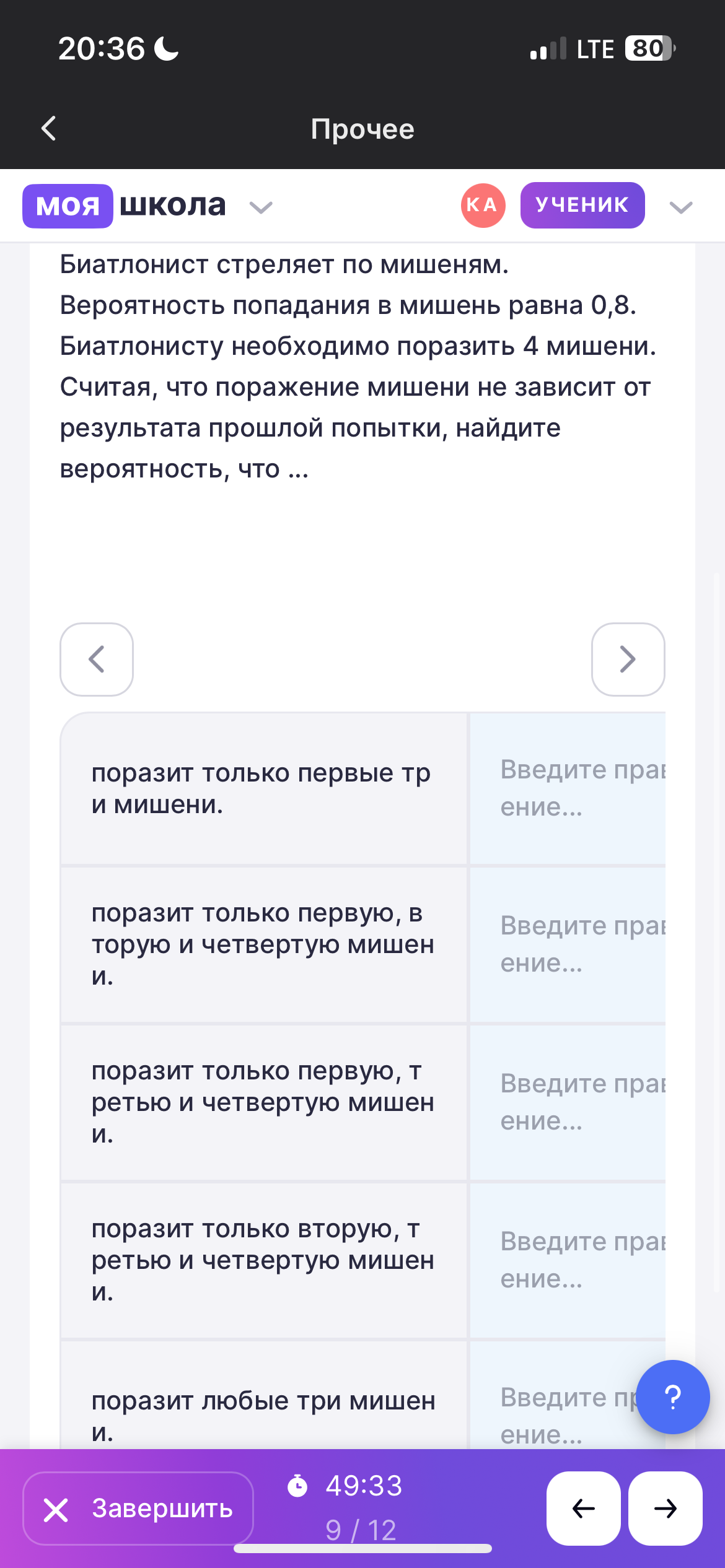
Биатлонист стреляет по мишеням. Вероятность попадания в мишень равна 0,8. Биатлонисту необходимо поразить 4 мишени. Считая, что поражение мишени не зависит от результата прошлой попытки, найдите вероятность, что поразит только вторую, третью и четвертую мишени.

Вероятность попадания в мишень равна 0.8, значит, вероятность промаха равна 1 - 0.8 = 0.2. Нам нужно, чтобы вторая, третья и четвертая мишени были поражены, а первая была промахом. Так как попадания независимы, мы можем перемножить вероятности: (P = 0.2 cdot 0.8 cdot 0.8 cdot 0.8 = 0.8^3 cdot 0.2 = 0.512 cdot 0.2 = 0.1024) Ответ: 0.1024