Вопрос:
Буксир прошёл 4 км по течению реки и 3 км против течения, затратив на путь по течению на 4 мин меньше, чем на путь против течения. Найдите собственную скорость буксира, если скорость течения реки составляет 3 км/ч.
Ответ:
\[Пусть\ x\ \frac{км}{ч} - собственная\ \]
\[скорость\ буксира;\]
\[(x + 3)\ \frac{км}{ч} - скорость\ \]
\[по\ течению;\ \]
\[(x - 3)\ \frac{км}{ч} - скорость\ \]
\[против\ течения.\]
\[4\ мин = \frac{1}{15}\ ч - шел\ меньше\ \]
\[по\ течению,\ чем\ против\ \]
\[течения.\]
\[Составим\ уравнение:\ \]
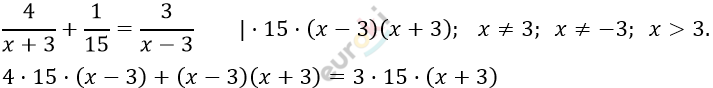
\[60x - 180 + x^{2} - 9 =\]
\[= 45x + 135\]
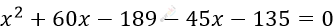
\[x^{2} + 15x - 324 = 0\]
\[x_{1} + x_{2} = - 15;\ \ x_{1} \cdot x_{2} = - 324\]
\[x_{1} = 12\ \left( \frac{км}{ч} \right) - собственная\ \]
\[скорость\ буксира.\ \ \]
\[x_{2} = - 27\ (не\ подходит).\]
\[Ответ:12\ \frac{км}{ч}.\]
Похожие
- Бригада рабочих должна была изготовить 900 деталей. В связи с болезнью одного из рабочих каждому из работавших пришлось изготовить на 10 деталей больше, чем планировалось. Сколько рабочих в полном составе бригады?
- Знаменатель обыкновенной дроби на 11 больше её числителя. Если числитель этой дроби увеличить на 1, а знаменатель уменьшить на 2, то полученная дробь будет на 1/9 больше исходной. Найдите исходную дробь.
- Катер прошёл 20 км по озеру, а затем 44 км по реке, вытекающей из этого озера, за 3 ч. Найдите собственную скорость катера, если скорость течения реки составляет 2 км/ч.