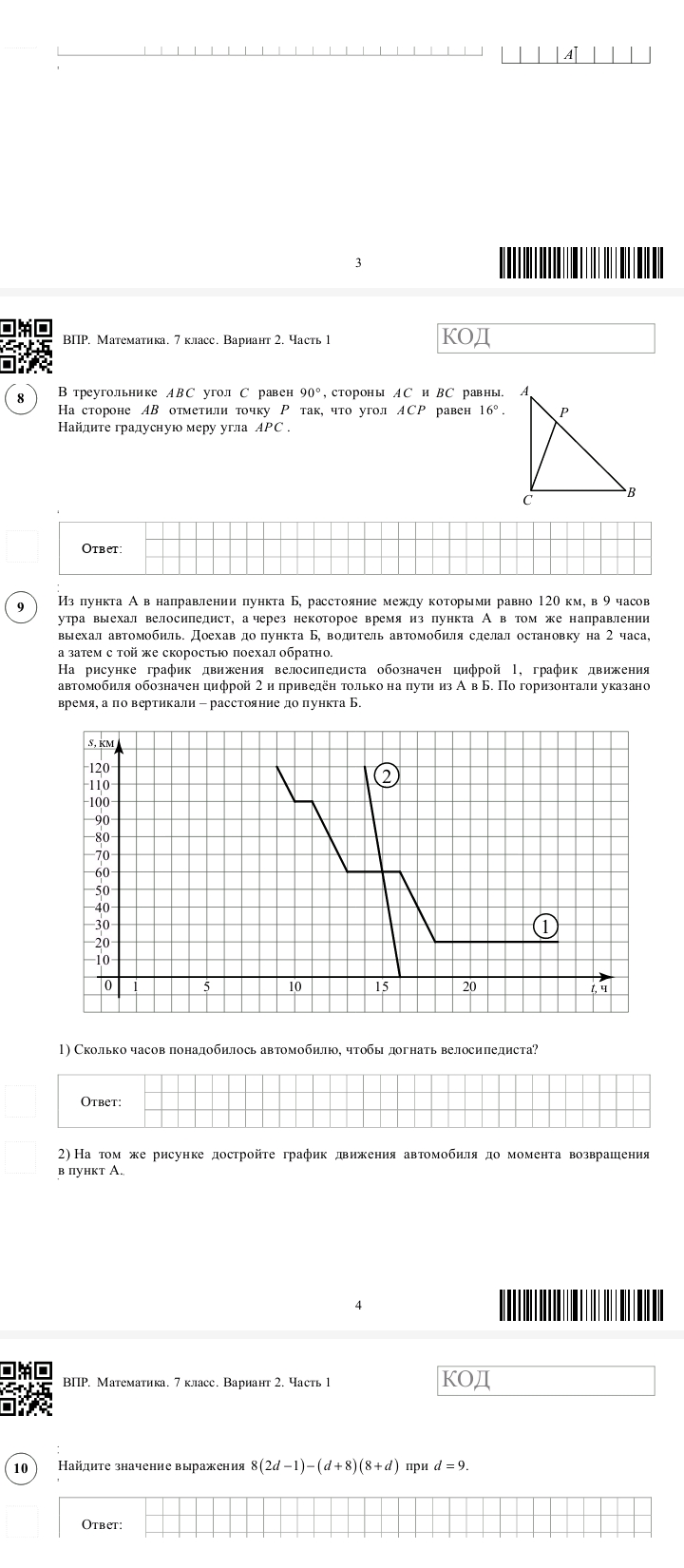
В треугольнике \(ABC\) угол \(C\) равен \(90°\), стороны \(AC\) и \(BC\) равны. На стороне \(AB\) отметили точку \(P\) так, что угол \(ACP\) равен \(16°\). Найдите градусную меру угла \(APC\).

Так как треугольник \(ABC\) прямоугольный и \(AC = BC\), то угол \(CAB\) равен \(45°\). Угол \(CAP\) является частью угла \(CAB\), и он образуется вычитанием угла \(PAC\) из угла \(CAB\). \(CAP = CAB - PAC = 45° - 16° = 29°\) В треугольнике \(APC\) сумма углов равна \(180°\). Угол \(APC = 180° - (90° + 16°)\) или \(180° - (90° + 29°)\) Угол \(APC = 180° - (90° + 29°) = 180° - 119° = 61°\). Ответ: 61°