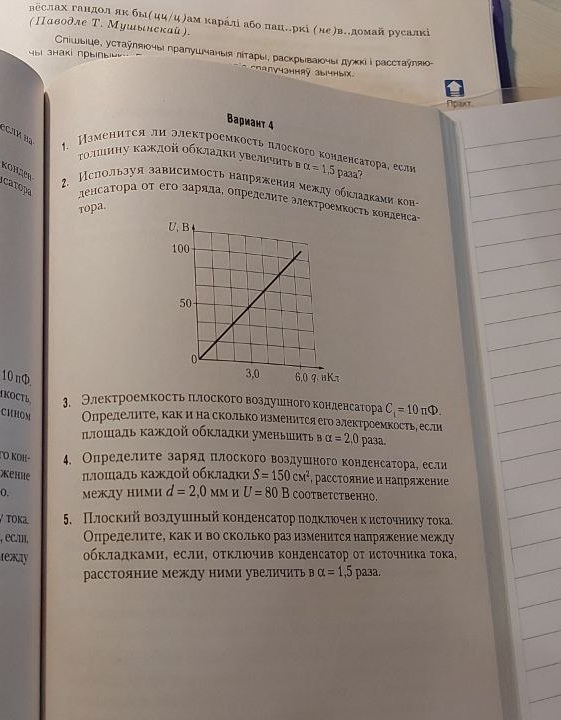
Задача 3: Электроемкость плоского воздушного конденсатора \(C_1 = 10 \text{ пФ}\). Определите, как и на сколько изменится его электроемкость, если площадь каждой обкладки уменьшить в \(\alpha = 2,0\) раза.

Электроемкость плоского конденсатора пропорциональна площади обкладок: \(C = \varepsilon_0 \frac{S}{d}\) Если площадь уменьшить в \(\alpha = 2\) раза, то новая электроемкость \(C_2\) будет: \(C_2 = \varepsilon_0 \frac{S/\alpha}{d} = \frac{1}{\alpha} \cdot \varepsilon_0 \frac{S}{d} = \frac{C_1}{\alpha}\) Подставим значения: \(C_2 = \frac{10 \text{ пФ}}{2} = 5 \text{ пФ}\) Изменение электроемкости: \(\Delta C = C_2 - C_1 = 5 \text{ пФ} - 10 \text{ пФ} = -5 \text{ пФ}\) Электроемкость уменьшится на 5 пФ. **Ответ:** Электроемкость уменьшится в 2 раза и станет равной 5 пФ.