Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
Математика
Вопрос:
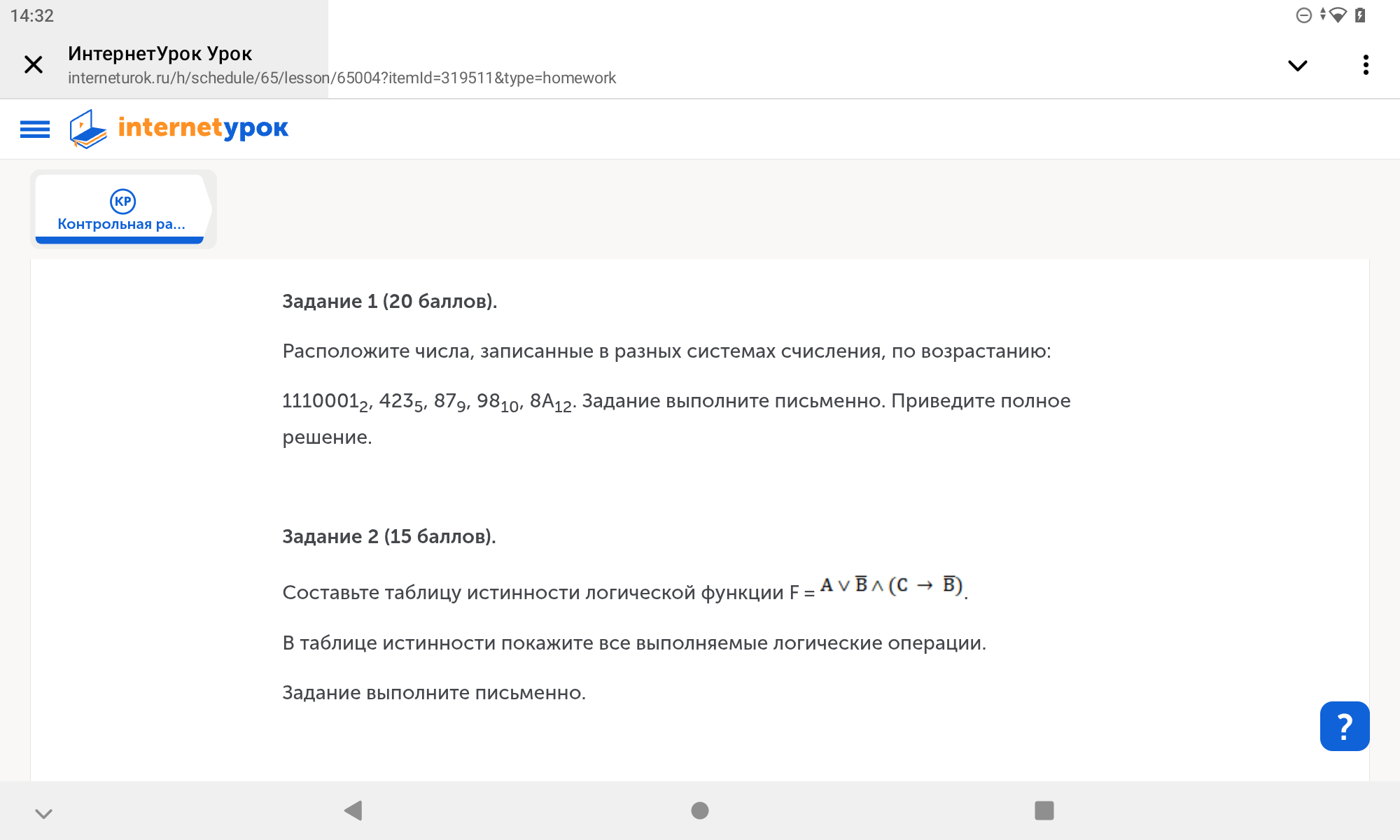
Задание 2 (15 баллов). Составьте таблицу истинности логической функции F = A ∨ ¬B ∧ (C → ¬B) В таблице истинности покажите все выполняемые логические операции. Задание выполните письменно.
Ответ:
Для построения таблицы истинности логической функции $$F = A \lor
eg B \land (C \rightarrow
eg B)$$, нам потребуется учесть все возможные комбинации значений A, B и C (0 или 1), а также выполнить логические операции в правильном порядке.
Таблица истинности:
| A | B | C | ¬B | C → ¬B | ¬B ∧ (C → ¬B) | A ∨ (¬B ∧ (C → ¬B)) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 |
Пояснения к таблице:
- ¬B: инверсия B (если B = 0, то ¬B = 1, и наоборот).
- C → ¬B: импликация (если C = 1, то ¬B должно быть 1, иначе результат 0; если C = 0, то результат всегда 1).
- ¬B ∧ (C → ¬B): конъюнкция (логическое И) между ¬B и результатом импликации. Результат равен 1, только если оба операнда равны 1.
- A ∨ (¬B ∧ (C → ¬B)): дизъюнкция (логическое ИЛИ) между A и результатом конъюнкции. Результат равен 1, если хотя бы один из операндов равен 1.
Ответ: Таблица истинности для функции F = A ∨ ¬B ∧ (C → ¬B) представлена выше.
Похожие
- Задание 1 (20 баллов). Расположите числа, записанные в разных системах счисления, по возрастанию: 11100012, 4235, 879, 9810, 8А12. Задание выполните письменно. Приведите полное решение.
- Задание 2 (15 баллов). Составьте таблицу истинности логической функции F = A ∨ ¬B ∧ (C → ¬B) В таблице истинности покажите все выполняемые логические операции. Задание выполните письменно.
