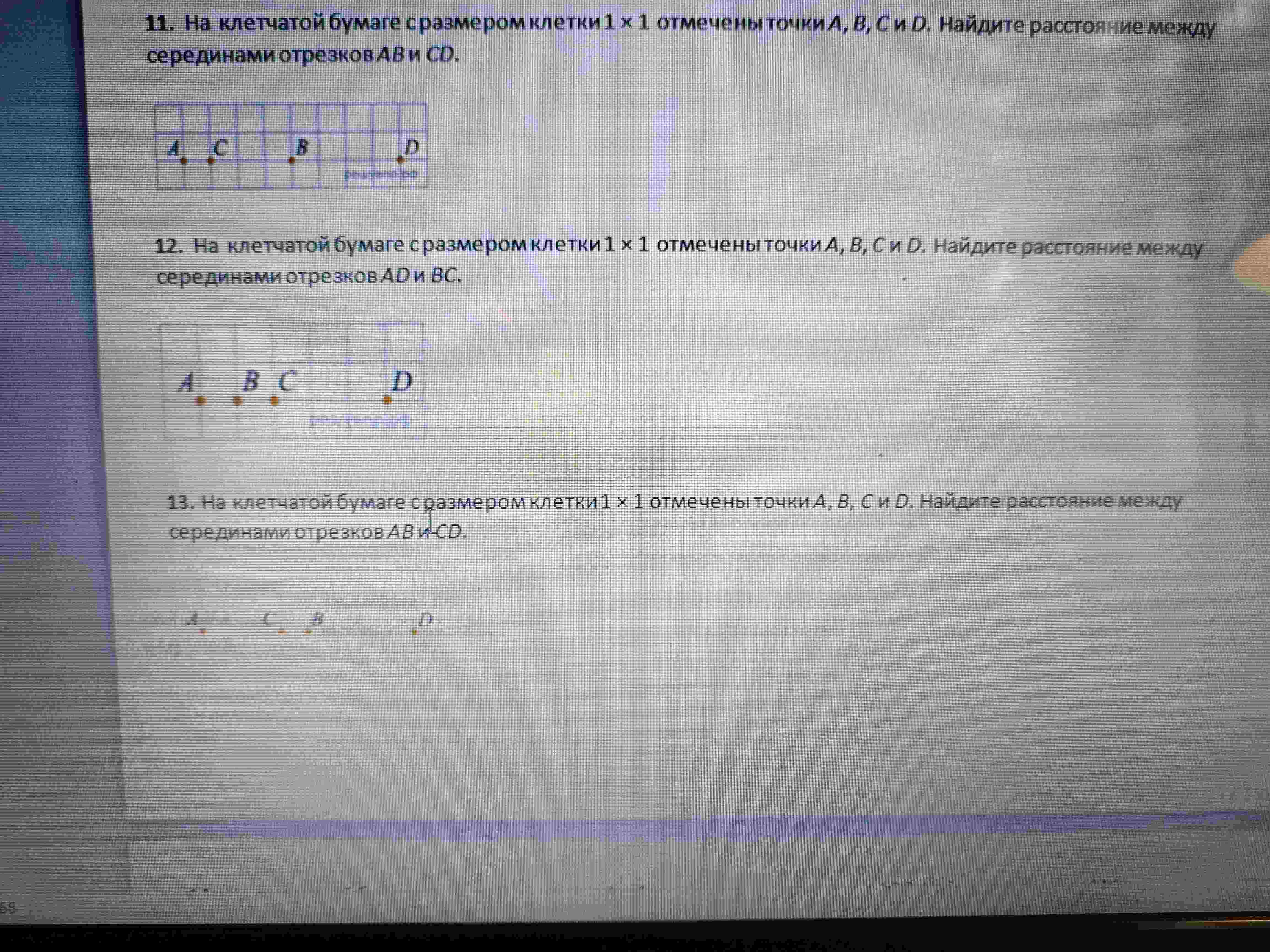
Вопрос:
13. На клетчатой бумаге с размером клетки 1 х 1 отмечены точки А, В, С и D. Найдите расстояние между серединами отрезков АВ и CD.
Ответ:
По аналогии с предыдущими задачами, определим координаты точек и найдем середины отрезков AB и CD, чтобы вычислить расстояние между ними.
* Определение координат точек:
* A(1, 1)
* B(4, 1)
* C(2, 1)
* D(5, 1)
* Нахождение середины отрезка AB (точка M):
\[M(\frac{x_A + x_B}{2}, \frac{y_A + y_B}{2})\]
\[M(\frac{1 + 4}{2}, \frac{1 + 1}{2}) = M(2.5, 1)\]
* Нахождение середины отрезка CD (точка N):
\[N(\frac{x_C + x_D}{2}, \frac{y_C + y_D}{2})\]
\[N(\frac{2 + 5}{2}, \frac{1 + 1}{2}) = N(3.5, 1)\]
* Нахождение расстояния между точками M и N:
\[d = \sqrt{(x_N - x_M)^2 + (y_N - y_M)^2}\]
\[d = \sqrt{(3.5 - 2.5)^2 + (1 - 1)^2}\]
\[d = \sqrt{1^2 + 0^2}\]
\[d = \sqrt{1}\]
\[d = 1\]
Ответ: 1
Похожие
- 11. На клетчатой бумаге с размером клетки 1 х 1 отмечены точки А, В, С и D. Найдите расстояние между серединами отрезков АВ и CD.
- 12. На клетчатой бумаге с размером клетки 1 х 1 отмечены точки А, В, С и D. Найдите расстояние между серединами отрезков AD и BC.
- 13. На клетчатой бумаге с размером клетки 1 х 1 отмечены точки А, В, С и D. Найдите расстояние между серединами отрезков АВ и CD.