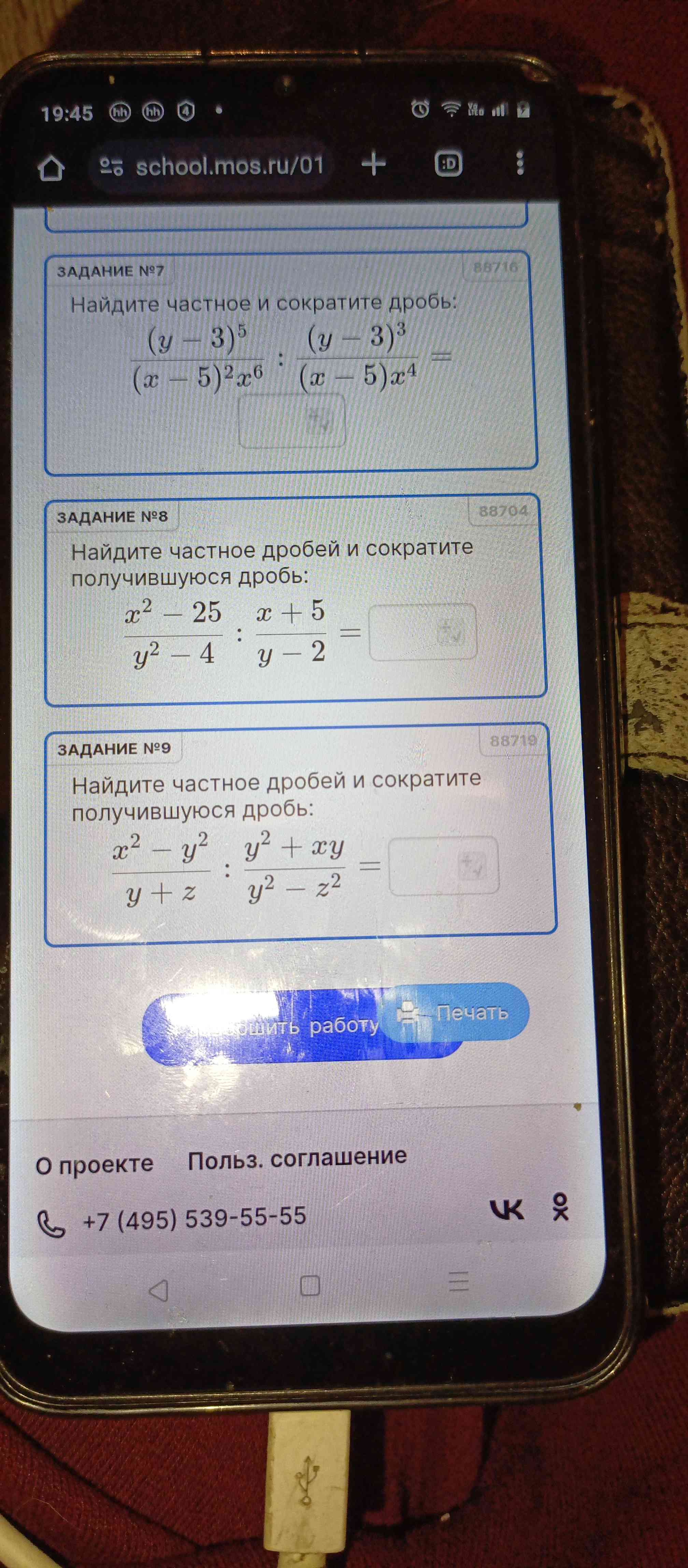
Вопрос:
Найдите частное дробей и сократите получившуюся дробь: $$\frac{x^2-y^2}{y+z} : \frac{y^2+xy}{y^2-z^2}$$
Ответ:
Для решения этого задания, необходимо разделить первую дробь на вторую. Деление дробей эквивалентно умножению первой дроби на дробь, обратную второй.
$$\frac{x^2-y^2}{y+z} : \frac{y^2+xy}{y^2-z^2} = \frac{x^2-y^2}{y+z} \cdot \frac{y^2-z^2}{y^2+xy}$$
Разложим числитель первой дроби и числитель второй дроби на множители, используя формулу разности квадратов: $$a^2 - b^2 = (a - b)(a + b)$$. Также вынесем общий множитель во второй дроби.
$$\frac{x^2-y^2}{y+z} \cdot \frac{y^2-z^2}{y^2+xy} = \frac{(x-y)(x+y)}{y+z} \cdot \frac{(y-z)(y+z)}{y(y+x)}$$
Теперь можно сократить дроби. $$(x+y)$$ и $$(y+x)$$ одинаковы, $$(y+z)$$ сокращается.
$$\frac{(x-y)(x+y)}{y+z} \cdot \frac{(y-z)(y+z)}{y(y+x)} = \frac{(x-y)(y-z)}{y}$$
Ответ: $$\frac{(x-y)(y-z)}{y}$$