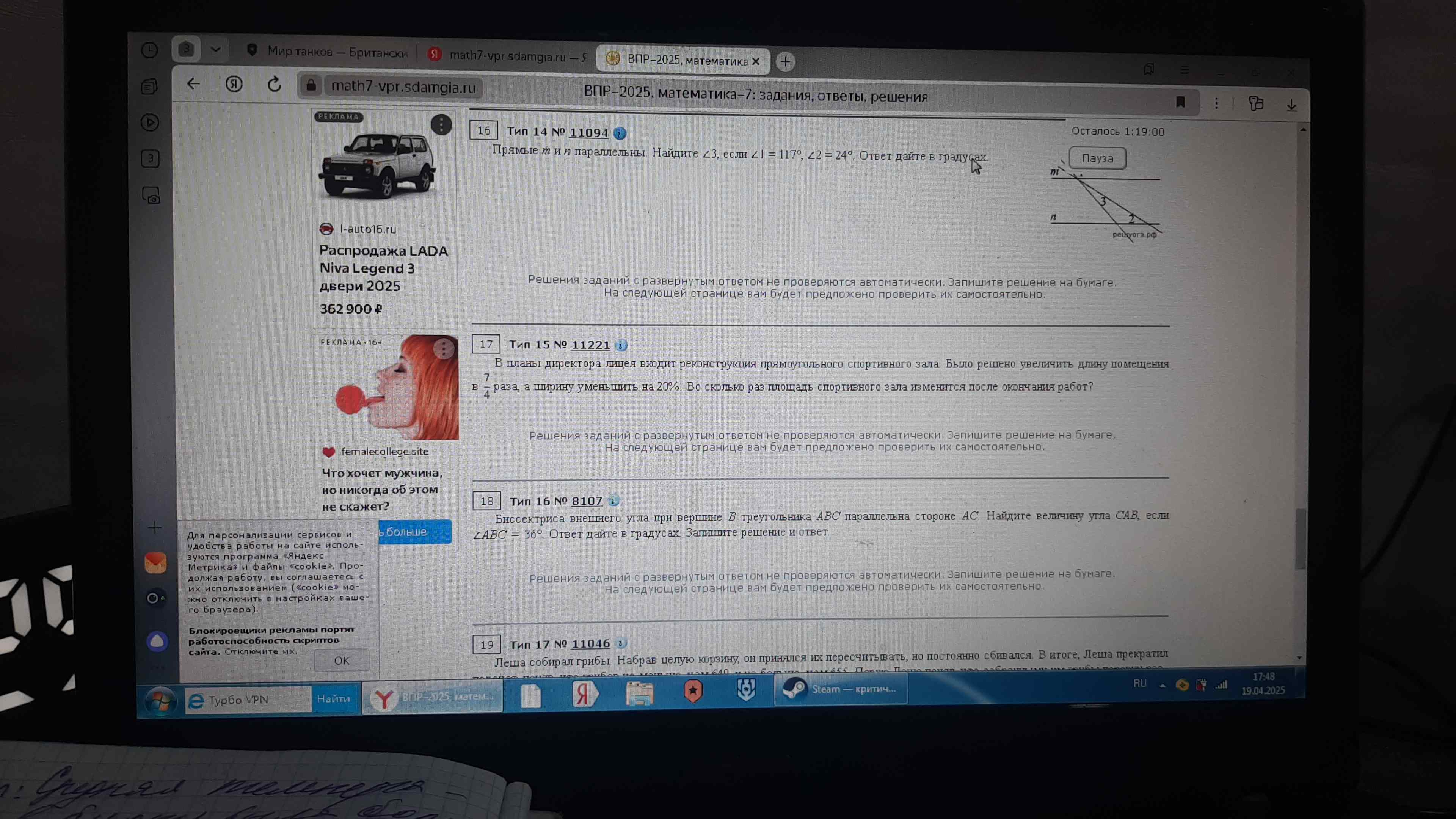
Тип 14 № 11094 Прямые m и n параллельны. Найдите $$\angle 3$$, если $$\angle 1 = 117^\circ$$, $$\angle 2 = 24^\circ$$. Ответ дайте в градусах.

Давайте решим эту задачу по геометрии. 1. Понимание задачи: У нас есть две параллельные прямые (m и n), и угол $$\angle 3$$ образован пересечением этих прямых с другой линией. Мы знаем величины углов $$\angle 1$$ и $$\angle 2$$. 2. Нахождение решения: \begin{itemize} \item{Угол $$\angle 1$$ и угол, смежный с углом $$\angle 3$$, являются соответственными углами при параллельных прямых m и n. Поэтому, смежный с углом $$\angle 3$$ угол равен $$\angle 1 = 117^\circ$$.} \item{Угол $$\angle 3$$ и угол $$24^\circ$$ ($$\angle 2$$) вместе составляют угол, смежный с углом $$\angle 1$$. Следовательно, $$\angle 3 + \angle 2 = 117^\circ$$.} \item{Теперь мы можем найти $$\angle 3$$: $$\angle 3 = 117^\circ - \angle 2 = 117^\circ - 24^\circ = 93^\circ$$.} \end{itemize} 3. Ответ: $$\angle 3 = 93^\circ$$. Ответ: 93