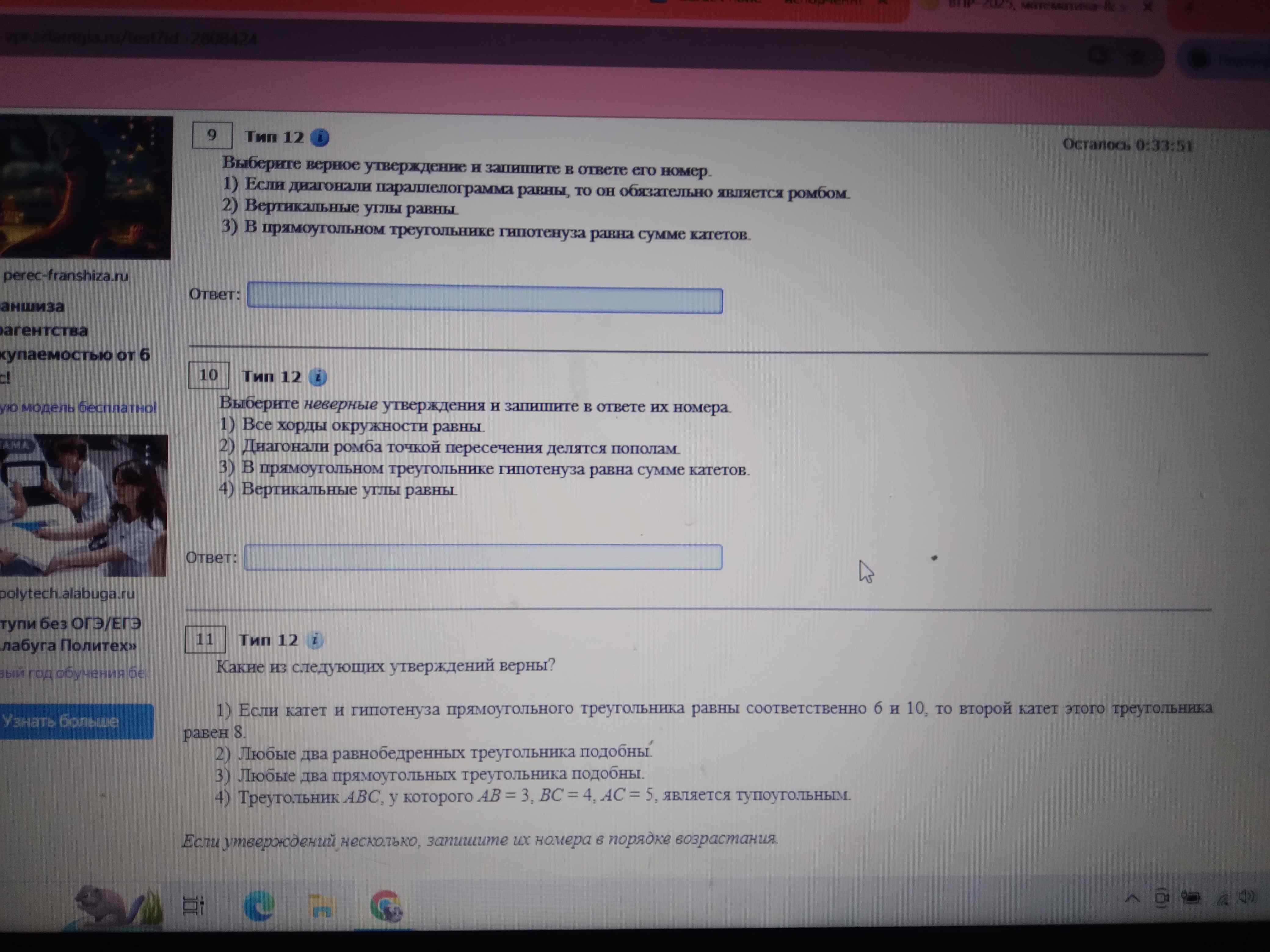
11. Тип 12. Какие из следующих утверждений верны? 1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8. 2) Любые два равнобедренных треугольника подобны. 3) Любые два прямоугольных треугольника подобны. 4) Треугольник \(ABC\), у которого \(AB = 3\), \(BC = 4\), \(AC = 5\), является тупоугольным.

Здравствуйте, ученики! Давайте проанализируем каждое утверждение: 1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8. Проверим это с помощью теоремы Пифагора: \[a^2 + b^2 = c^2\]\[6^2 + b^2 = 10^2\]\[36 + b^2 = 100\]\[b^2 = 100 - 36\]\[b^2 = 64\]\[b = \sqrt{64} = 8\] Это утверждение верно. 2) Любые два равнобедренных треугольника подобны. Это неверно. У равнобедренных треугольников должны быть равны углы при основании. 3) Любые два прямоугольных треугольника подобны. Это неверно. У прямоугольных треугольников должен быть хотя бы один острый угол равным. 4) Треугольник \(ABC\), у которого \(AB = 3\), \(BC = 4\), \(AC = 5\), является тупоугольным. Проверим, выполняется ли теорема Пифагора: \[3^2 + 4^2 = 9 + 16 = 25\]\[5^2 = 25\] Так как \(3^2 + 4^2 = 5^2\), то треугольник является прямоугольным, а не тупоугольным. Это утверждение неверно. Итак, верно только утверждение 1. Ответ: 1