Вопрос:
Выбери верное разложение на множители 25x<sup>4</sup>-40x<sup>2</sup>y + 16y<sup>2</sup> =
Ответ:
Заметим, что данное выражение похоже на квадрат разности: $$(a - b)^2 = a^2 - 2ab + b^2$$.
В нашем случае: $$25x^4 - 40x^2y + 16y^2 = (5x^2)^2 - 2 \cdot 5x^2 \cdot 4y + (4y)^2$$.
Следовательно, выражение можно представить как: $$(5x^2 - 4y)^2$$.
Ответ: (5x2-4y)2
Похожие
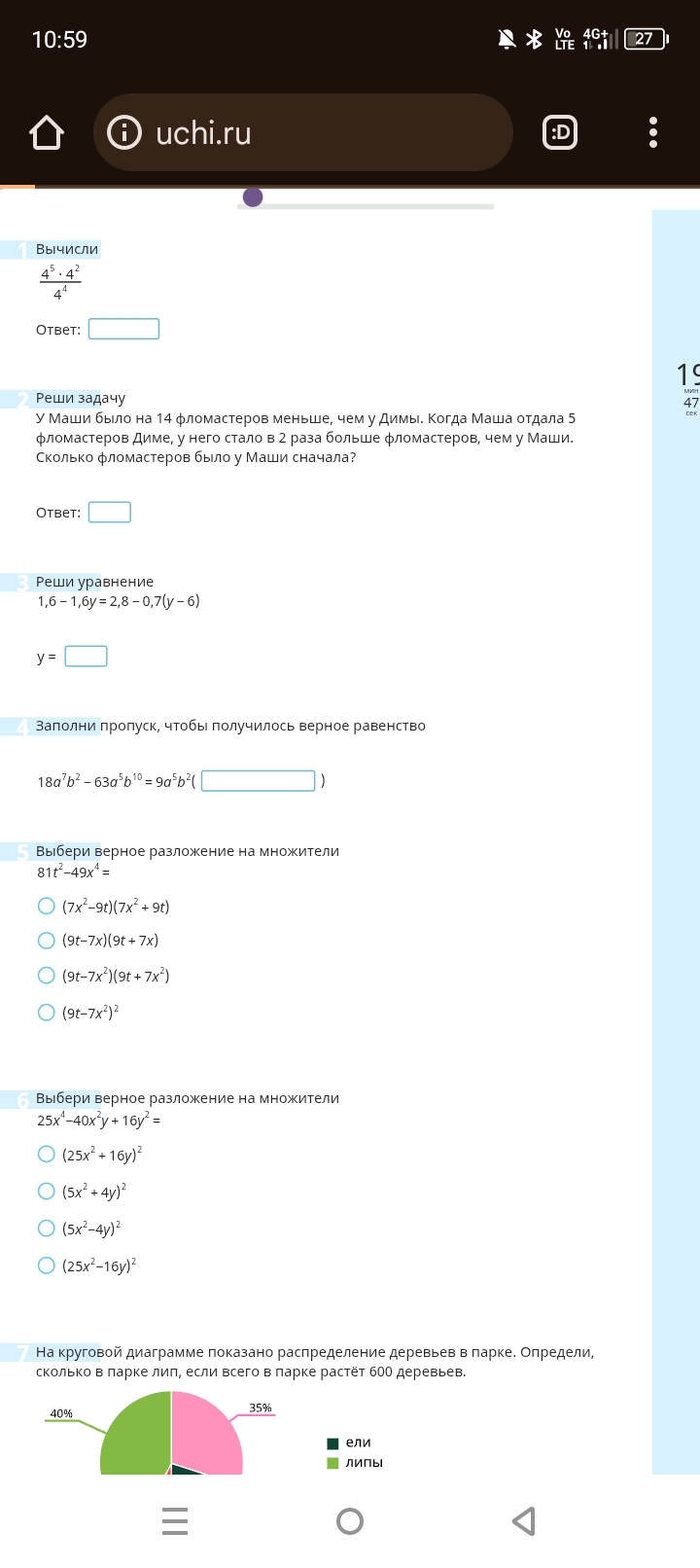
- Вычисли $$\frac{4^5 \cdot 4^2}{4^4}$$ Ответ:
- Реши задачу У Маши было на 14 фломастеров меньше, чем у Димы. Когда Маша отдала 5 фломастеров Диме, у него стало в 2 раза больше фломастеров, чем у Маши. Сколько фломастеров было у Маши сначала? Ответ:
- Реши уравнение 1,6 - 1,6y = 2,8 - 0,7(y - 6) y =
- Заполни пропуск, чтобы получилось верное равенство 18a<sup>7</sup>b<sup>2</sup> - 63a<sup>5</sup>b<sup>10</sup> = 9a<sup>5</sup>b<sup>2</sup>(...)
- Выбери верное разложение на множители 81t<sup>2</sup>-49x<sup>4</sup> =
- Выбери верное разложение на множители 25x<sup>4</sup>-40x<sup>2</sup>y + 16y<sup>2</sup> =
- На круговой диаграмме показано распределение деревьев в парке. Определи, сколько в парке лип, если всего в парке растёт 600 деревьев.