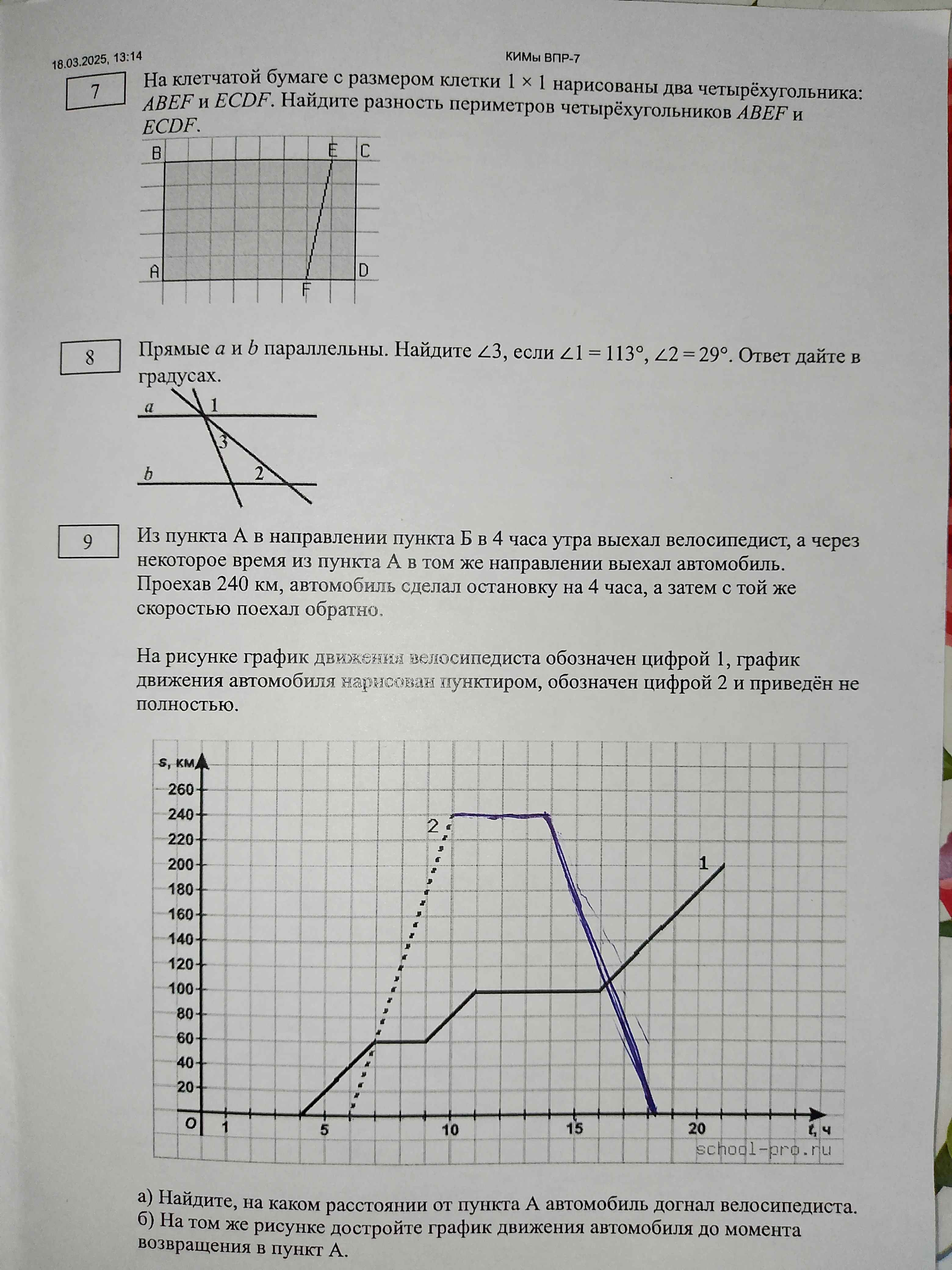
Задание 7. На клетчатой бумаге с размером клетки 1 × 1 нарисованы два четырёхугольника: ABEF и ECDF. Найдите разность периметров четырёхугольников ABEF и ECDF.

Чтобы найти разность периметров, нужно сначала определить длины сторон каждого четырехугольника. Поскольку у нас клетчатая бумага с размером клетки 1x1, мы можем посчитать длины сторон по клеткам. Четырехугольник ABEF: AB = 5 (клеток) BE = 4 (клетки) EF = √((2-5)^2 + (4-1)^2) = √(9 + 9) = √18 = 3√2 (по теореме Пифагора) FA = 3 (клетки) Периметр ABEF = 5 + 4 + 3√2 + 3 = 12 + 3√2 Четырехугольник ECDF: EC = 5 (клеток) CD = 3 (клетки) DF = 1 (клетки) FE = √((5-2)^2 + (4-1)^2) = √(9 + 9) = √18 = 3√2 (по теореме Пифагора) Периметр ECDF = 5 + 3 + 1 + 3√2 = 9 + 3√2 Разность периметров = (12 + 3√2) - (9 + 3√2) = 12 - 9 + 3√2 - 3√2 = 3 Ответ: 3