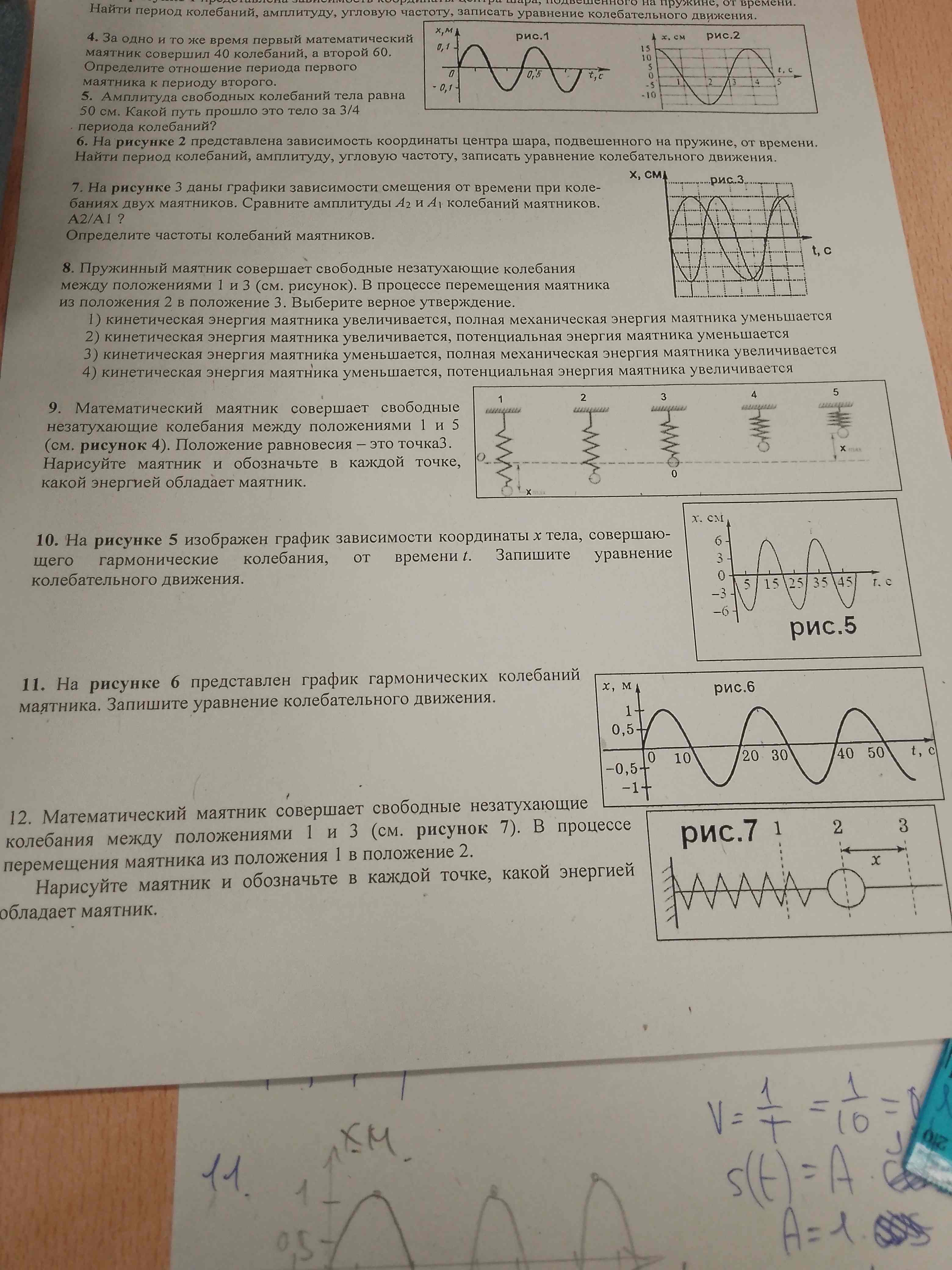
10. На рисунке 5 изображен график зависимости координаты x тела, совершающего гармонические колебания, от времени t. Запишите уравнение колебательного движения.

Для решения этой задачи используем график на рисунке 5. * **Период (T)**: По графику видно, что одно полное колебание занимает 20 секунд (например, от максимума в 5 с до максимума в 25 с). Таким образом, T = 20 с. * **Амплитуда (A)**: Максимальное отклонение от положения равновесия (нуля) равно 6 см, что составляет 0.06 м. Таким образом, A = 0.06 м. * **Угловая частота (\(\omega\))**: Рассчитывается по формуле \(\omega = \frac{2\pi}{T}\). Подставляем значение периода: \(\omega = \frac{2\pi}{20} = \frac{\pi}{10}\) рад/с. * **Уравнение колебательного движения**: Имеет вид \(x(t) = A \cos(\omega t + \phi_0)\), где \(\phi_0\) - начальная фаза. В нашем случае, в начальный момент времени (t=0) координата равна 3, а не амплитуде (6), значит, начальная фаза \(\phi_0 = \frac{\pi}{3}\). Таким образом, уравнение имеет вид: \(x(t) = 0.06 \cos(\frac{\pi}{10}t + \frac{\pi}{3})\). **Ответ:** Уравнение колебательного движения: \(x(t) = 0.06 \cos(\frac{\pi}{10}t + \frac{\pi}{3})\).