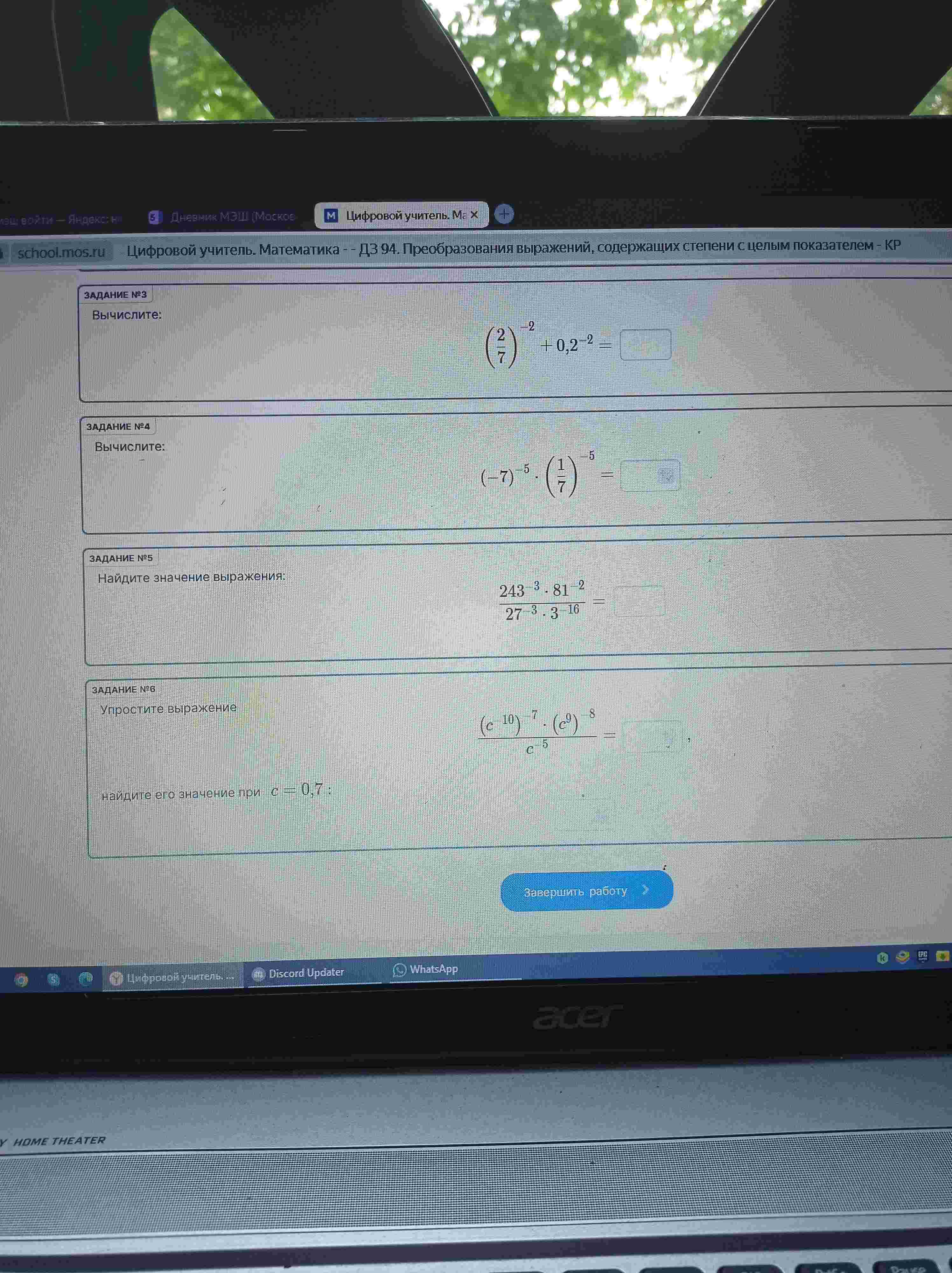
ЗАДАНИЕ №6 Упростите выражение $$\frac{(c^{10})^7 \cdot (c^9)^8}{c^{-5}} =$$ найдите его значение при $$c = 0,7$$:

Сначала упростим выражение, используя свойства степеней: $$(a^m)^n = a^{m \cdot n}$$ и $$\frac{a^m}{a^n} = a^{m-n}$$. $$\frac{(c^{10})^7 \cdot (c^9)^8}{c^{-5}} = \frac{c^{10 \cdot 7} \cdot c^{9 \cdot 8}}{c^{-5}} = \frac{c^{70} \cdot c^{72}}{c^{-5}} = \frac{c^{70+72}}{c^{-5}} = \frac{c^{142}}{c^{-5}} = c^{142 - (-5)} = c^{142+5} = c^{147}$$ Теперь найдем значение выражения при $$c = 0,7$$: $$c^{147} = (0,7)^{147}$$. Это очень маленькое число, и его сложно представить в виде обыкновенной дроби или десятичного числа. Ответ: $$(0,7)^{147}$$