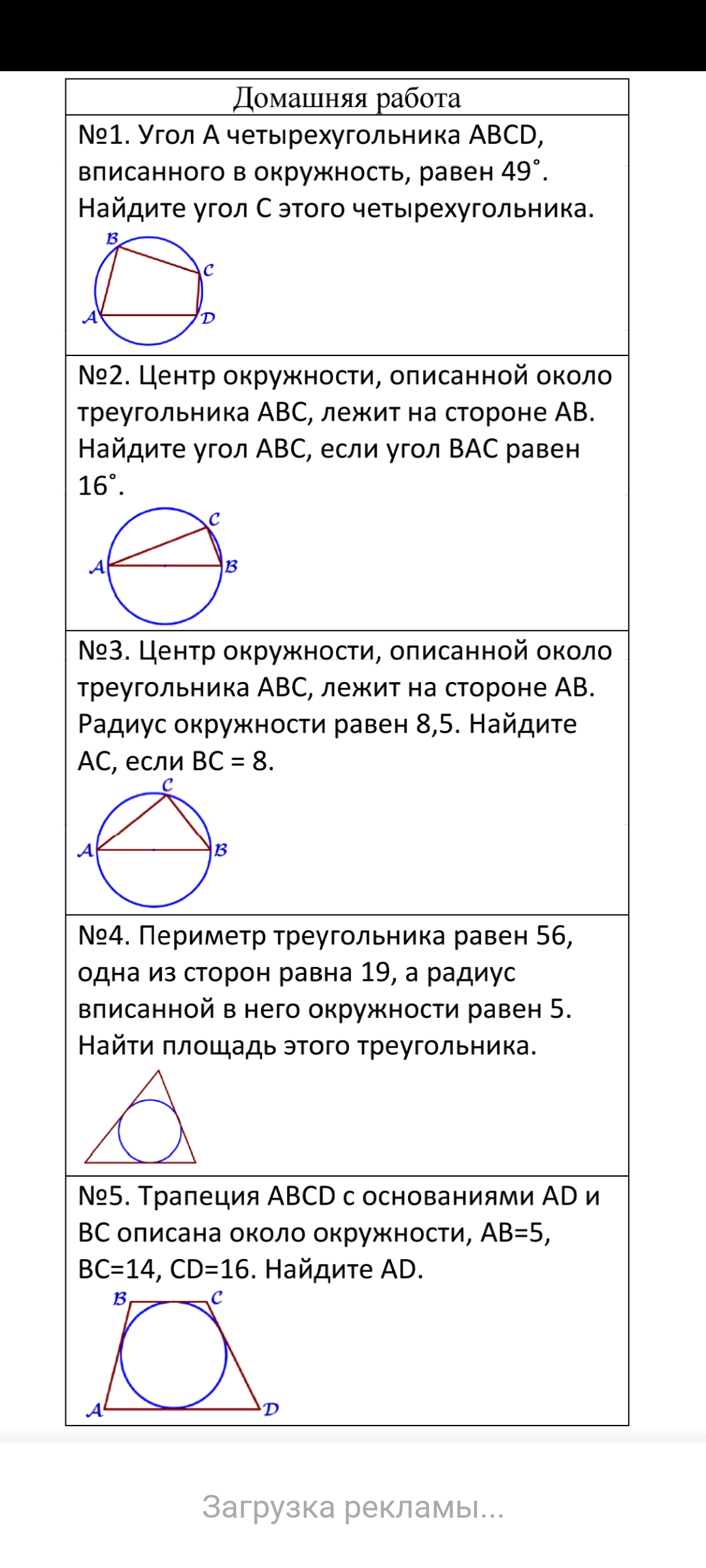
№3. Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 8,5. Найдите АС, если ВС = 8.

Поскольку центр окружности, описанной около треугольника ABC, лежит на стороне AB, это означает, что AB является диаметром окружности. Следовательно, треугольник ABC — прямоугольный, с углом ACB равным 90 градусам.

Так как радиус окружности равен 8,5, то диаметр AB равен 2 * 8,5 = 17.

Теперь у нас есть прямоугольный треугольник ABC, где:

• AB (гипотенуза) = 17
• BC (катет) = 8
• AC (катет) - нужно найти

Используем теорему Пифагора: $$AC^2 + BC^2 = AB^2$$

Подставим известные значения:

$$AC^2 + 8^2 = 17^2$$Вычислим:

$$AC^2 + 64 = 289$$Решим уравнение для AC:

$$AC^2 = 289 - 64$$Ответ: 15