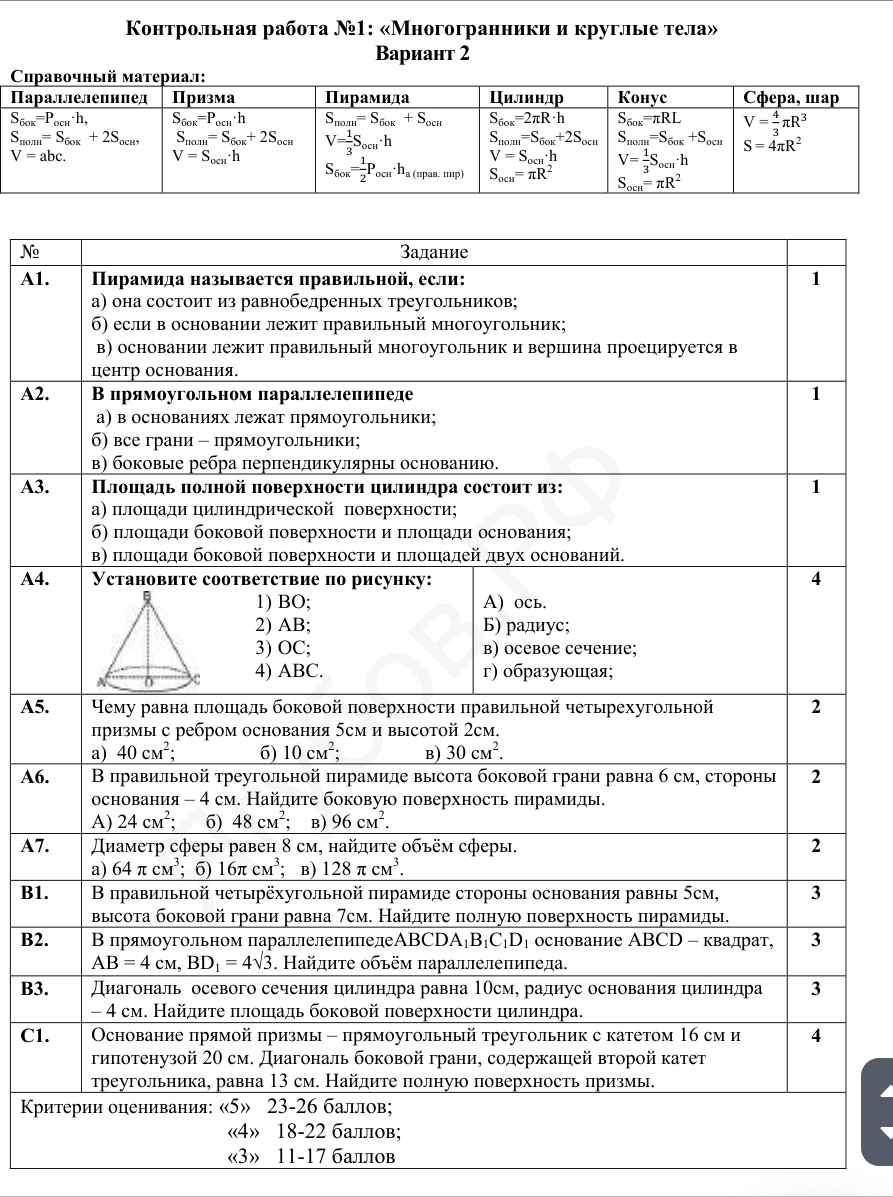
C1. Основание прямой призмы прямоугольный треугольник с катетом 16 см и гипотенузой 20 см. Диагональ боковой грани, содержащей второй катет треугольника, равна 13 см. Найдите полную поверхность призмы.

Катет a = 16 см. Гипотенуза c = 20 см. Второй катет b = √(c² - a²) = √(20² - 16²) = √(400 - 256) = √144 = 12 см. Диагональ боковой грани d = 13 см (содержит катет b). Высота призмы h = √(d² - b²) = √(13² - 12²) = √(169 - 144) = √25 = 5 см. Площадь основания S_осн = (1/2) * a * b = (1/2) * 16 * 12 = 96 см². Площадь боковой поверхности S_бок = P_осн * h = (a + b + c) * h = (16 + 12 + 20) * 5 = 48 * 5 = 240 см². Полная поверхность призмы S_полн = 2 * S_осн + S_бок = 2 * 96 + 240 = 192 + 240 = 432 см². Ответ: 432 см²