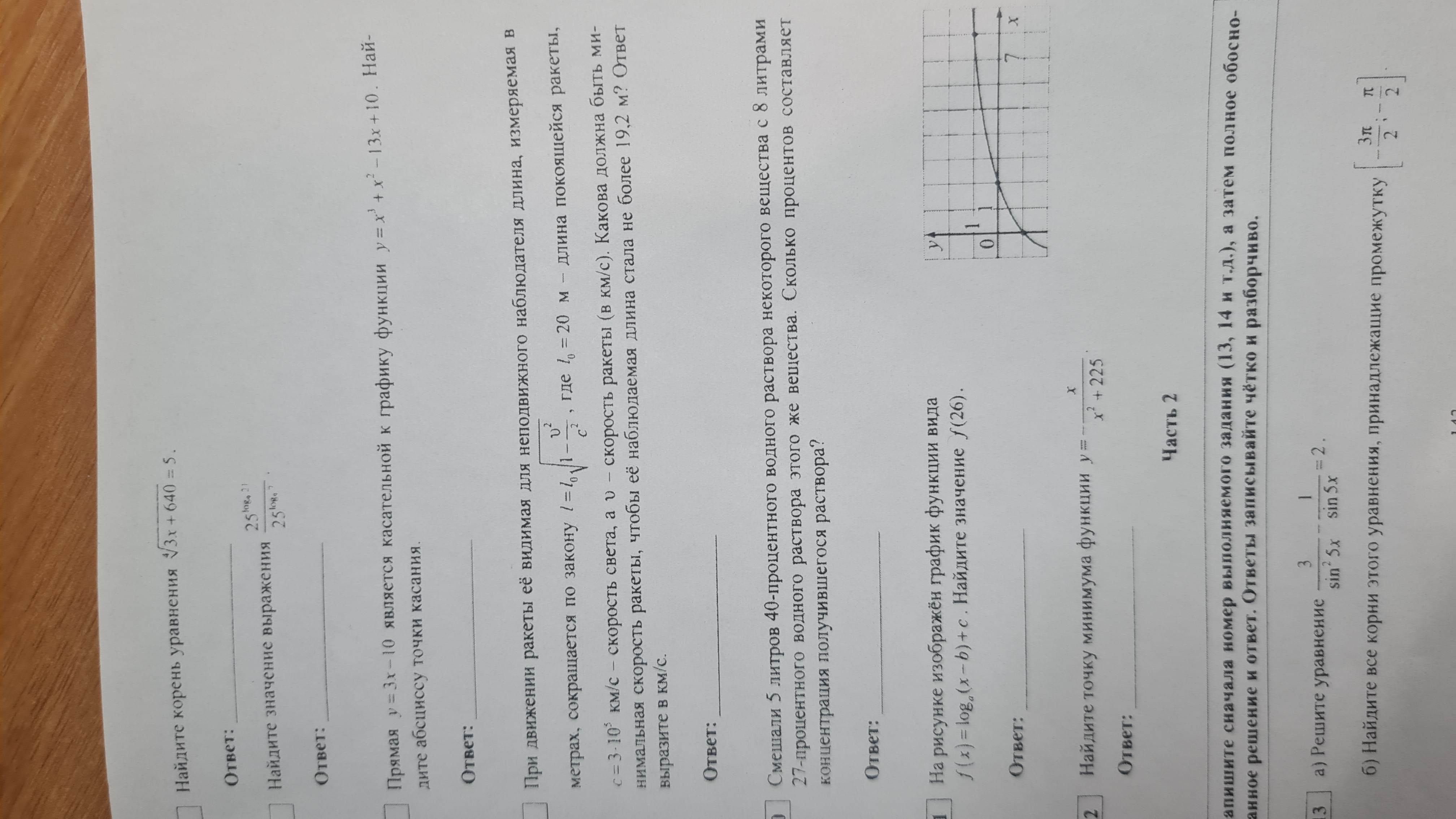
Прямая \(y = 3x - 10\) является касательной к графику функции \(y = x^3 + x^2 - 13x + 10\). Найдите абсциссу точки касания.

**Решение:** 1. Найдем производную функции \(y = x^3 + x^2 - 13x + 10\). \[y' = 3x^2 + 2x - 13\] 2. Производная функции в точке касания равна угловому коэффициенту касательной. Угловой коэффициент касательной \(y = 3x - 10\) равен 3. Следовательно, \[3x^2 + 2x - 13 = 3\] 3. Решим уравнение \(3x^2 + 2x - 13 = 3\): \[3x^2 + 2x - 16 = 0\] 4. Найдем дискриминант: \[D = b^2 - 4ac = 2^2 - 4 \cdot 3 \cdot (-16) = 4 + 192 = 196\] 5. Найдем корни уравнения: \[x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-2 + \sqrt{196}}{2 \cdot 3} = \frac{-2 + 14}{6} = \frac{12}{6} = 2\] \[x_2 = \frac{-b - \sqrt{D}}{2a} = \frac{-2 - \sqrt{196}}{2 \cdot 3} = \frac{-2 - 14}{6} = \frac{-16}{6} = -\frac{8}{3}\] 6. Проверим, какая из точек является точкой касания. Для этого подставим найденные значения \(x\) в уравнение касательной и исходной функции и убедимся, что значения \(y\) совпадают. * Для \(x = 2\): * Касательная: \(y = 3(2) - 10 = 6 - 10 = -4\) * Функция: \(y = (2)^3 + (2)^2 - 13(2) + 10 = 8 + 4 - 26 + 10 = -4\) Значения совпадают, значит, \(x=2\) - абсцисса точки касания. * Для \(x = -\frac{8}{3}\): * Касательная: \(y = 3(-\frac{8}{3}) - 10 = -8 - 10 = -18\) * Функция: \(y = (-\frac{8}{3})^3 + (-\frac{8}{3})^2 - 13(-\frac{8}{3}) + 10 = -\frac{512}{27} + \frac{64}{9} + \frac{104}{3} + 10 = \frac{-512 + 192 + 936 + 270}{27} = \frac{886}{27} \approx 32.8\) Значения не совпадают, значит, \(x=-\frac{8}{3}\) не является абсциссой точки касания. **Ответ:** 2