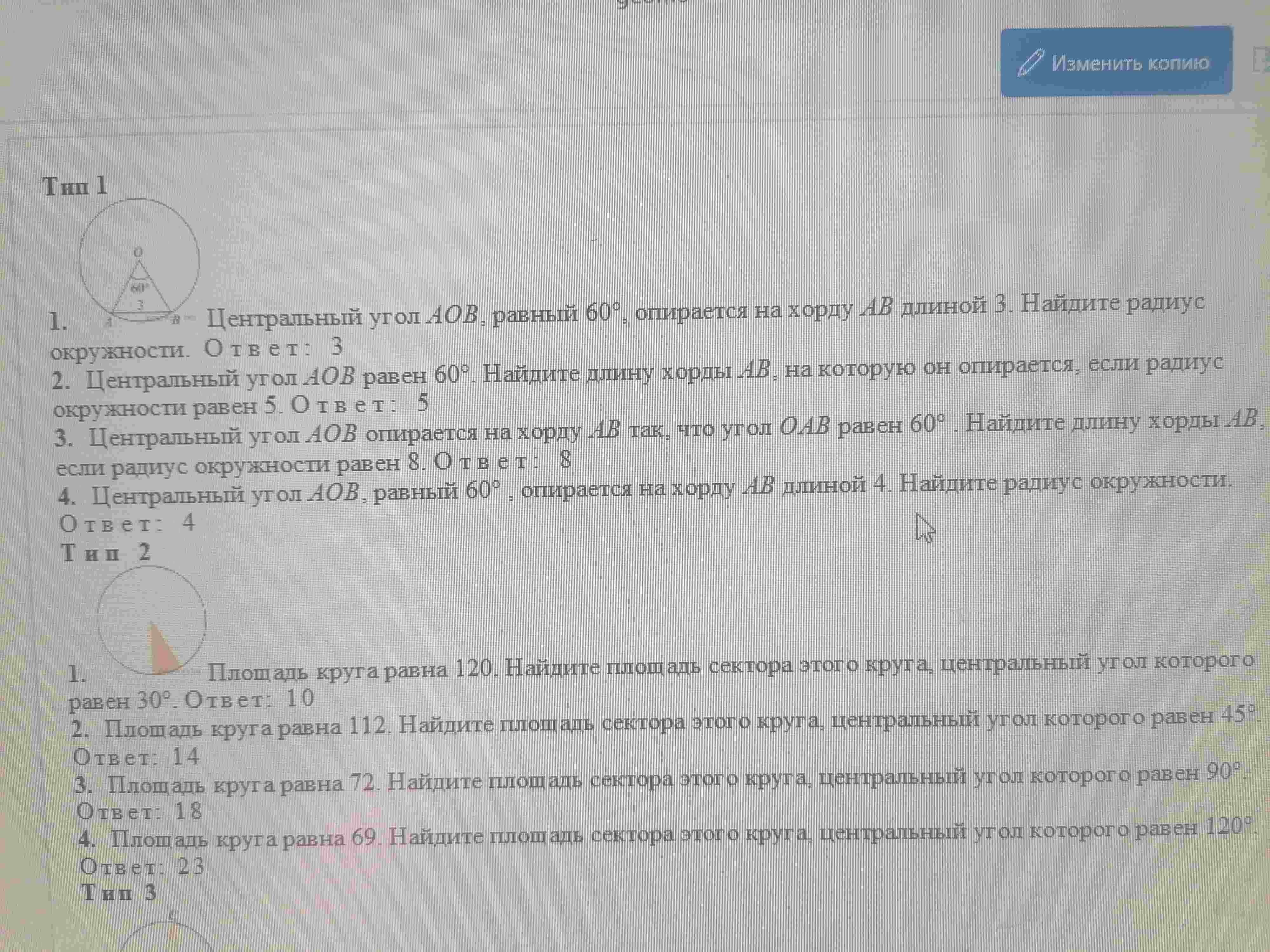
Вопрос:
Тип 1, задача 3: Центральный угол \(AOB\) опирается на хорду \(AB\) так, что угол \(OAB\) равен \(60^\circ\). Найдите длину хорды \(AB\), если радиус окружности равен 8.
Ответ:
Так как угол \(OAB\) равен \(60^\circ\) и треугольник \(AOB\) равнобедренный (\(OA = OB\) как радиусы), то угол \(OBA\) также равен \(60^\circ\). Следовательно, угол \(AOB\) равен \(180^\circ - 60^\circ - 60^\circ = 60^\circ\). Таким образом, треугольник \(AOB\) равносторонний, и длина хорды \(AB\) равна радиусу окружности.
Ответ: 8
Похожие
- Тип 1, задача 1: Центральный угол \(AOB\) равен \(60^\circ\), опирается на хорду \(AB\) длиной 3. Найдите радиус окружности.
- Тип 1, задача 2: Центральный угол \(AOB\) равен \(60^\circ\). Найдите длину хорды \(AB\), на которую он опирается, если радиус окружности равен 5.
- Тип 1, задача 3: Центральный угол \(AOB\) опирается на хорду \(AB\) так, что угол \(OAB\) равен \(60^\circ\). Найдите длину хорды \(AB\), если радиус окружности равен 8.
- Тип 1, задача 4: Центральный угол \(AOB\), равный \(60^\circ\), опирается на хорду \(AB\) длиной 4. Найдите радиус окружности.
- Тип 2, задача 1: Площадь круга равна 120. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
- Тип 2, задача 2: Площадь круга равна 112. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
- Тип 2, задача 3: Площадь круга равна 72. Найдите площадь сектора этого круга, центральный угол которого равен 90°.
- Тип 2, задача 4: Площадь круга равна 69. Найдите площадь сектора этого круга, центральный угол которого равен 120°.