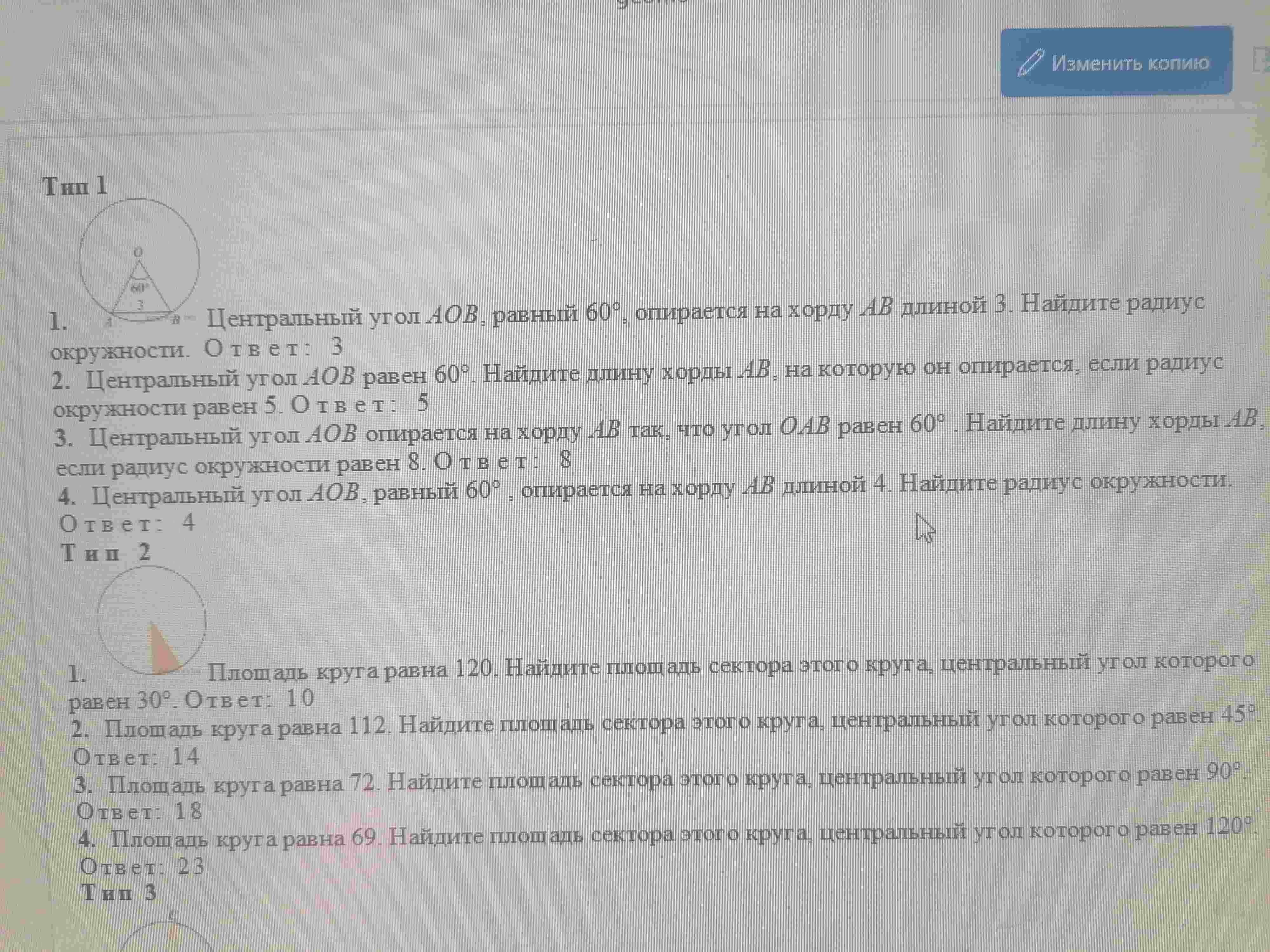
Тип 1, задача 4: Центральный угол \(AOB\), равный \(60^\circ\), опирается на хорду \(AB\) длиной 4. Найдите радиус окружности.

Поскольку центральный угол \(AOB\) равен \(60^\circ\), а стороны \(OA\) и \(OB\) равны радиусу окружности, треугольник \(AOB\) является равнобедренным. Так как один из углов равен \(60^\circ\), то и остальные углы также равны \(60^\circ\), что делает его равносторонним. Следовательно, радиус окружности равен длине хорды \(AB\). Ответ: 4